Warning: this post is a bit wonkish. Math ahead! 

Controlling the Covid-19 pandemic requires testing and contact tracing, but the usefulness of tests declines if getting results takes too long: a week is no longer unusual, and there have been reports of three week waits. Given that the standard PCR tests, which try to identify viral RNA in the sample, involve sophisticated biochemistry that requires ingredients that are in limited supply, one wonders: aren’t there simpler, faster tests? There are: antigen tests, which instead look for viral proteins. But the problem is that they are not as good: the false-positive or the false-negative rate is substantially higher than for a good PCR test. To see why that matters, and how to overcome this problem, we need to discuss what a positive test result even means, which is best done within the framework of Bayes’ theorem from probability theory. I will not discuss or even prove it here, but you can find an excellent intuitive discussion by 3blue1brown, who made an awesome video about this. I can’t possibly compete with his clarity, so I’ll just urge you to look it up. If you don’t already know what Bayes’ theorem is, these are 15 minutes and 45 seconds that are incredibly well spent.

OK, here we go. 

Assume we have a test that can identify Covid-19. Of course, at times the test gets it wrong, and there are two different ways for how this could happen: either a person who is sick is erroneously told that they are healthy (a false negative), or a healthy person is erroneously told that they are sick (a false positive). Ideally, these rates are small, but they are never zero. How do they affect how we interpret the outcome of a test?

The key problem is that we have not accounted for the prevalence of the disease. If the disease is rare, then most people who are tested are in fact healthy. And even if the sick ones are found out pretty reliably, among the large number of healthy people we will accumulate a sizable number of false positives. The problem is that we can’t tell the false positives from the true positives. They are just positive test results. What we want to know is: if you tested positive, what are the odds that you are actually sick? Meaning, that in the group of true and false positives, you are a true positive?

That’s where the theorem of Bayes comes in. It permits us to answer the question “what’s the probability someone is sick, given that they tested positive?” Notice that this question is something like the “inverse” version of what we know about the test quality, namely, “what’s the probability that someone tests positive, given that they are sick?” The key thing is that these two probabilities are not the same, but that Bayes’ theorem helps us to get one from the other. It says:

$$P(C|+) = \frac{P(+|C)\;P(C)}{P(+)} \ .$$

Let’s parse this: $P(C)$ is the probability of being sick (the “$C$” reminds us of “Covid-19”), and $P(+)$ is the probability of ending up with a positive test result. The expression $P(C|+)$ is the so-called conditional probability of being sick, given that one tested positive, and the expression $P(+|C)$ is the inverse conditional probability of testing positive, given that one is sick. Just remember that the vertical bar is pronounced “given that”, and it is easy to read.

Sidenote: If you’re still uncomfortable about the two conditional probailities not being equal, imagine rolling a dice and being interested in the two outcomes “I got a 6”, versus “I got an even (“E”) number”. I’m sure you can very quickly convince yourself that $P(6|\textrm{E})=1/3$ and $P(\textrm{E}|6)=1$, and so they are obviously not the same.

To answer our question, let us look at the following so-called probability tree:

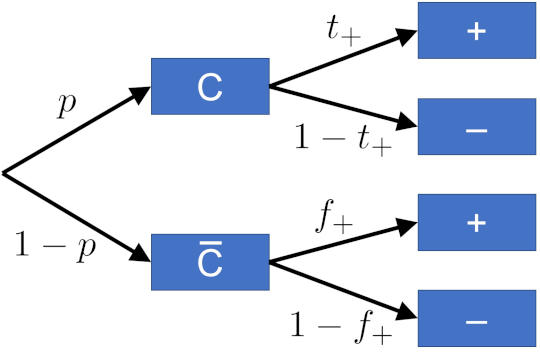
Here’s how we read it. Start from the left, where you meet a first bifurcation: a person could either have Covid-19 ($C$), or not ($\overline{C}$) (the bar over the letter is a shorthand to denote negation: not Covid-19.) The letters next to the arrows indicate the probability of that happening: $p$ being the probability of the person being sick, and $1-p$ the probability for being healthy. Each of these two outcomes now has a second branch point: if we now test, will the test come back positive or not? This depends on whether the person has the disease or not. If the person is sick, a positive outcome happens with probability $t_+$, the true positive rate, while the probability of accidentally getting a negative result is $1-t_+$; if instead the person is healthy, a positive outcome can still happen, but with the (hopefully much smaller) false positive rate $f_+$, while the probability for a negative outcome, $1-f_+$, is ideally much higher.

Sidenote: there’s another bit of lingo possibly worth knowing about. In medical diagnostics, the true positive rate is called the “sensitivity” of the test: the ability to pick up the disease if it’s there. And the complement of the false positive rate ($1-f_+=t_-$, the true negative rate!) is called the “specificity” of the test: it’s ability to correctly identify those who don’t have the disease, or alternatively, to not be fooled into a positive result by something that looks similar (like a similar looking version of a different virus).

We’re now ready for our first big question: what is the probability that a person who enters the test center gets a positive test? There are two ways for how this could happen: the person could be sick, and the test says so; or the person could be healthy, but the test gets it wrong. The probability for each of these scenarios is calculated by multiplying the probabilities “along the way”, and the total probability is merely the sum of those two probabilities. We hence find:

$$\begin{align}P(+) &= P(C) P(+|C) + P(\overline{C}) P(+|\overline{C}) \\[1em] &= p t_+ + (1-p) f_+ \ . \end{align}$$

We now have everything we need to calculate the odds of a person being sick if the test comes back positive. Using Bayes’ theorem, we get

$$\begin{align}P(C|+) &= \frac{P(+|C)P(C)}{P(+)}\\[0.5em] &= \frac{p t_+}{p t_+ + (1-p) f_+}\\[0.5em] &= \frac{1}{1+\displaystyle\frac{1-p}{p}\times\displaystyle\frac{f_+}{t_+}} \ .\end{align}$$

Ideally, we want this probability to be large. This is the case when the second term in the denominator is small, or, equivalently, if $(1-p) f_+ \ll pt_+$. Now, if the disease is rare, $p$ is small, and then $1-p$ is close to one. Also, if the test is good, the true positive rate is close to one. Making these two simplifying assumptions, this inequality becomes $f_+ \ll p$, which says that for a good test the false positive rate has to be small compared to the prevalence of the disease. It’s not enough to be “small compared to 1”. It must be small compares to $p$, and this could be a difficult thing to achieve if the disease is rare.

Let us now apply this to the Covid-19 case. Assume we have a pretty good test, with 1% false positive and false negative rate, and let us consider the case that 5% of the people entering the testing site actually have Covid-19. If one of them gets a positive test result, what are the odds they are actually sick? From what we’ve seen above in the general case, we simply need to put in numbers:

$$\begin{align}P(C|+) &= \frac{1}{1+\displaystyle\frac{(1-p) f_+}{p t_+}}\\[0.5em] &= \frac{1}{1+\displaystyle\frac{0.95\cdot0.01}{0.05\cdot0.99}}\\[1em] &\approx 84\% \ .\end{align}$$

Does that strike you as surprising? The test seems really good, but the odds of having Covid-19 after testing positive are significantly smaller than the 99% one might initially have expected. But it gets worse: what if the test isn’t quite so good? Specifically, antigen tests might have false positive and false negative rates in the 10% range (or worse, but let’s stick with 10%). If we use these numbers instead, what are now the odds that a positive Covid-19 tests actually correctly identifies the disease? Let’s calculate:

$$\begin{align}P(C|+) &= \frac{1}{1+\displaystyle\frac{(1-p) f_+}{p t_+}}\\[0.5em] &= \frac{1}{1+\displaystyle\frac{0.95\cdot0.10}{0.05\cdot0.90}}\\[1em] &\approx 32\% \ .\end{align}$$

That’s pretty terrible. Yes, you might get your answer in minutes, but if the odds of being sick is actually only about 1 in 3, we’d be quarantining a lot of people for a long time (and scare them). And of course when we now contact-trace, we’ll run into a lot more people who will be falsely identified as sick. The speed of less reliable tests comes at a huge price.

However, there is a way to use cheap tests that offers a true benefit, and that is to use them as a pre-test, before we decide to actually run a more reliable but much slower test. Let’s see how that works. A simple way to do that is again with a probability diagram:

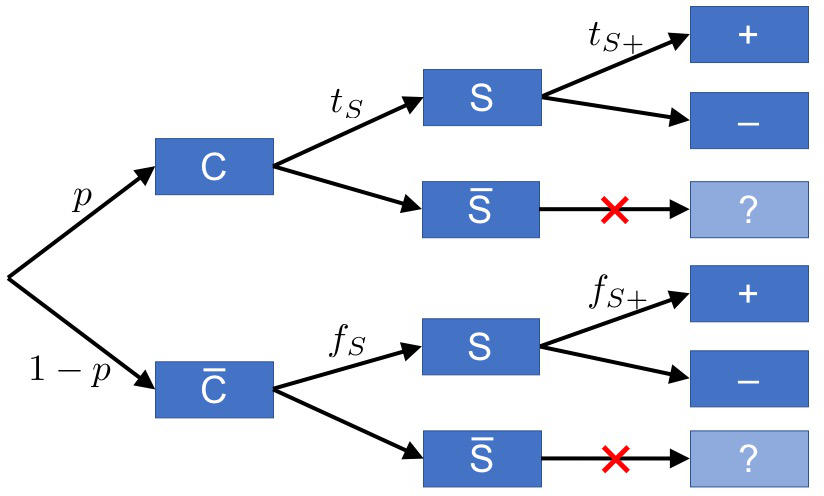
We again have the Covid-19 versus no Covid-19 branch; but before we do a good test, we do a quick and cheap pre-test. That test does not yet have a positive or negative outcome, just a “suspicious” ($S$) and a “not suspicious” ($\overline{S}$) one. The true and false suspicious rates, $t_S$ and $f_S$, are like the true and false positive rates of a poor test, but they only measure “suspicion”. Now, only if a person is identified as “suspicious”—and we know that within minutes, which is the benefit of a cheap and quick test—do we follow up with a full test, that strives to go for a “definitive” positive or negative. If the person is not suspicious, they can go. 

There’s a small catch, though, worth pointing out: The true and false positive rates we write at the last set of branches are not what we previously meant by the true and false positive rates for the better test. The reason is that we’re not testing everyone. We’re only testing the people who are already marked as “suspicious”, and so what we rather have is the conditional probabilities for true or false positives, given that the person was suspicious. That’s why we added the additional “S” to the symbol.

Now, if whatever gave rise to this “suspicious label” is entirely independent of the subsequent good test, then the conditional rates are identical to our previous rates (i.e., the ones without the extra “S” label). But it is more likely that there is a connection: if the pre-test declares a person as “suspicious”, it’s quite possible that the subsequent test will have an easier time to correctly identify the disease, or avoid an incorrect branding of a healthy individual that has been declared “not suspicious”. But it is also possible that the conditional probabilities are smaller than the non-conditional ones. For instance, if the “suspicious” test is particularly sensitive to some aspect of the disease that the subsequent good test is particularly likely to be confused about, then that good test might be performing worse (compared to the case where we didn’t actually pre-select for such a confusing situation).

For now, let us simply make sure we understand what these rates mean and hope that in a real-world scenario someone takes the time to determine them! 

We’re now ready to calculate the probability that in the two-stage testing scenario a person comes back with a positive test:

$$\begin{align}P(+) &= pt_S t_{S+} + (1-p)f_S f_{S+} \ .\end{align}$$

And this is what we need to get to the final question: what is the probability that a person with a positive test result actually has Covid-19? Using Bayes’ formula, we get

$$
\begin{align}
P(C|+) &= \frac{P(+|C)P(C)}{P(+)}\\[0.5em]
&= \frac{p t_S t_{S+}}{p t_S t_{S+}+(1-p) f_S f_{S+}}\\[0.5em] &= \frac{1}{ 1+\displaystyle\frac{1-p}{p}\times\frac{f_S f_{S+}}{t_S t_{S+}}} \ .
\end{align}
$$

Fun fact: observe that compared to the single-step test, which had the ratio $f_+/t_+$ in the denominator, this two-step test instead features the ratio $f_Sf_{S+}/t_St_{S+}$.

Time to put in numbers. Let us assume that the second test is the good one, and that the first test is mediocre, with false rates of 10%. The only thing we need to know is: what are the rates $t_{S+}$ and $f_{S+}$? The first is the true positive rate of a sick person who has been correctly identified as “suspicious”; the second is the false positive rate of someone who has incorrectly been identified as “suspicious”. As we had mentioned before, these need not coincide with the true and false positive rates, $t_+$ and $f_+$, from our initial scenario (i.e., the one without a pre-test); but in order to not complicate matters even further, let us assume that they do, and let us simply again use 99% for the true positive rate and 1% for the false positive rate.

We can now put in numbers:

$$\begin{align}P(C|+) &= \frac{1}{ 1+\displaystyle\frac{0.95\times 0.1\times 0.01}{0.05\times 0.9\times 0.99}}\\[1em] &= 97.9\% \ . \end{align}$$

We see that the probability has quite significantly increased, compared to just doing the good test alone. That is maybe not surprising, given that we have two test results to rely on, and even though the poor test is not very good, it adds a bit of extra confidence.

But is this always true?

One can indeed show: yes. Provided only that the pre-test satisfies one quite minimal sanity check: the true suspicious rate must be larger than the false suspicious rate, $t_S>f_S$. If that is not the case, then we deliberately send healthy people to get a full test and send sick people home without being tested—not a smart condition for getting a good overall test!

Interestingly, while the pre-test always improves matters, the extent of improvement depends on the situation, for instance the probability of the disease. The following plot illustrates this:

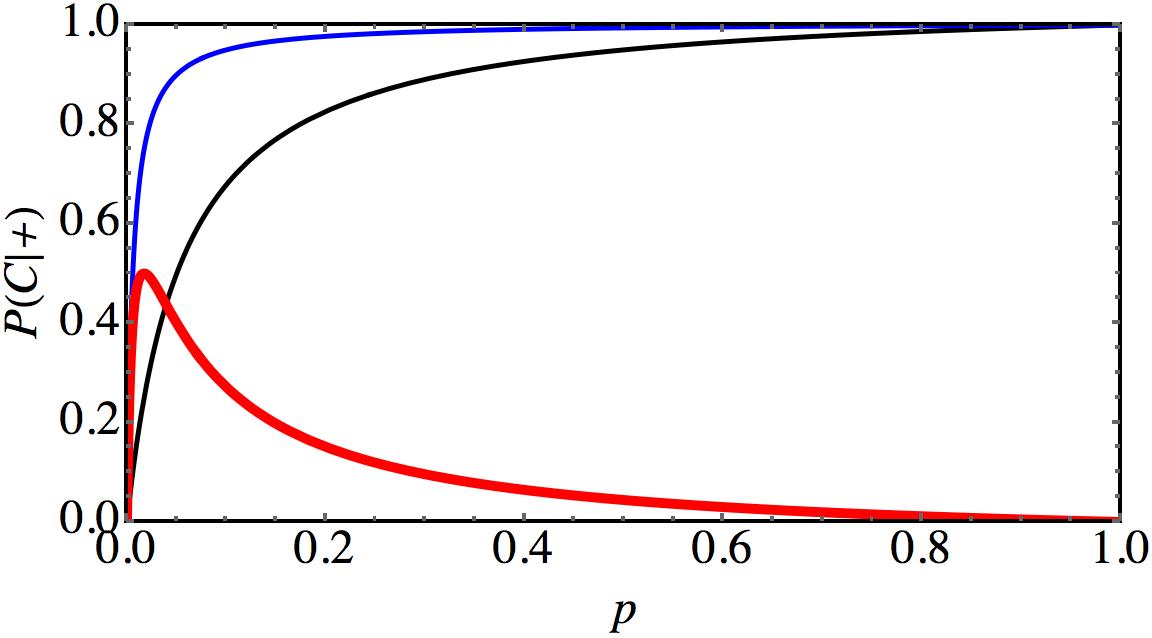
This graph shows $P(C|+)$ as a function of the disease probability $p$ if one only does the good test (black curve), if one does the good test after a pre-test (blue curve), and the difference between these two probabilities (red curve). For illustration purposes we assume that the “good” test is actually quite poor, with both false rates being 5%, and the pre-test having false rates of 10%. If the prevalence of the disease is also 5%, then the good test alone gives $P(C|+)=50\%$, which is pretty lousy. But with an extra pre-test this is bumped to an amazing $P(C|+)=90\%$, which corresponds to a single good test with false rates as low as 0.58%! A poor and a lousy test in series make an impressive test!

The biggest improvement would be seen if the disease probability were given by $p=1.7\%$, where we get a shift by 50 percentage points. For $p=5\%$ we “only” get a shift of 40 percentage points. Obviously, one could now try to adjust the quality of the tests such that the maximum is hit at the actual prevalence of the disease!

Getting a more accurate overall test is very pleasant. But there is also a second advantage of this two-tier procedure: we can cut down on the number of slow and expensive full tests. To see how this works, let us check how many good tests are even done. What is the probability that a person entering the testing center will also be subjected to a good (and hence slow and expensive) test? Evidently, this is the same as the probability that that person will be identified as “suspicious”:

$$\begin{align}P(S) &= pt_S + (1-p)f_S\\[1em] &= 0.05\times 0.9+0.95\times 0.1\\[1em] &= 14\%\ . \end{align}$$

This means that only about 1 in 7 people are given the slow test (with our example numbers from above), and so much fewer slow tests need to be done. That frees up resources, and that could help to make the test overall faster (say, because labs are no longer overwhelmed with tests). Hence, here we have a way to make the system more efficient by including a pre-test that filters out those that likely don’t need a full test.

Unfortunately, this system also has a downside: Since the poor test has a higher false negative rate as the good test, we will release more people back into the community who are actually sick. How many? If we apply the good test to everyone, then in this case the probability of sending somebody back who is sick is

$$P(-|C) = 1-t_+ = 1-0.99 = 1\%\ .$$

In the two-tier test we must add all those sick people who were erroneously identified as not suspicious, and therefore never received the full test. This gives

$$
\begin{align}
P(-|C)
&=
t_S(1-t_{S+}) + (1-t_S)\\[1em]
&=
0.9\times(1-0.99)+(1-0.9)\\[1em]&= 10.9\% \ .
\end{align}
$$

This is not good. The likelihood of sending sick people back into the community, where they might infect others, is ten times as high as if we had done a full test. Is this acceptable? This might depend on circumstances. But recall that if we had actually done a full test, we’d also have sent these people back into the community, and then they might only have learned a week later that they really must properly quarantine. Absent that conclusive answer, will they preemptively quarantine? Maybe not. Given that, it might be better to send these people back after a cheap test, but then simply check people with this improved protocol more regularly. After all, what looks like a 2-stage test is often really a 3-stage test: the people who enter the testing center often already have a suspicion, and that’s why they come in the first place. Say, they have a cough or a fever. Those coughing and feverish people who were deemed “not suspicious”, but who are actually sick, and who we nevertheless sent back into the community, might continue to have these symptoms and feel that something is off. And, truth be told, we haven’t told them they are negative; we just told them that a cheap pre-test has not found them “suspicious”. Now that we have removed a lot of strain on the system, we might actually be able to test them again,  just a few days later (much before the current timeline of a week for a full result), and get another good chance at catching the disease.

Evidently, models of this type can be extended a lot. We could add levels for symptoms, or we could think harder about how the two tests interact. The upshot is that there’s a lot of clever procedures we can do that exploit the mechanics of testing and probability. We should not be shy to think hard about this. Or at least listen, when epidemiologists have found a better way to test and contact trace. After all, it is in everybody’s interest to beat this virus as soon as possible.

Markus Deserno is a professor in the Department of Physics at Carnegie Mellon University. His field of study is theoretical and computational biophysics, with a focus on lipid membranes.