by Amirali Hossein

Biological lipid membranes divide eukaryotic cells into compartments with specialized functionality and play a central role in controlling the flow of matter and information between them. Their main building blocks are hundreds of different types of lipids, and the lipid composition of the two leaflets of many bilayer membranes is known to not be the same. This asymmetry is believed to be present in all domains of life and therefore ought to play an important functional role.

While there are various proteins responsible for transporting lipids between membrane leaflets and modifying their composition in complex ways, fundamentally, lipid bilayer asymmetry is possible due to the fact that the time-scale for spontaneous movement of a lipid from one leaflet to another (called “flip-flop”) is much longer than time-scales of many relevant biological processes.

In our previous work [Biophys. J. 118 (3), 624-642 (2020)], using coarse-grained molecular dynamics simulations we found that if we create a bilayer from two monolayers, each constituted of a single (different) type of lipid, we do not observe an increase in bilayer rigidity when the area accessible to lipids in each leaflet is the same as their preferred area in a symmetric bilayer. Instead, we suspected that the stiffening could be explained by the occurrence of an imbalance between the lateral tension present in the leaflets, what we refer to as “differential stress”. The net tension in lipid bilayers is almost always close to zero, however, there is no straightforward method to measure tension in individual leaflets and the difference in their stresses was assumed to be vanishing.

We found that if we create a large enough differential stress in a membrane by overfilling one leaflet and underfilling the other, we can observe an increase in bending rigidity of that membrane compared to one with the same total number of lipids that are distributed equally between the leaflets. The stiffness of the membranes was determined using the buckling method [J. Chem. Phys. 138, 214110 (2013)] which is based on the idea that if we laterally compress a membrane it would “buckle” (see Fig. 1), and the amount of force needed to be exerted for the membrane to be buckled to a specific amount could be determined by a theoretical formula if we treat the membrane as an elastic sheet.

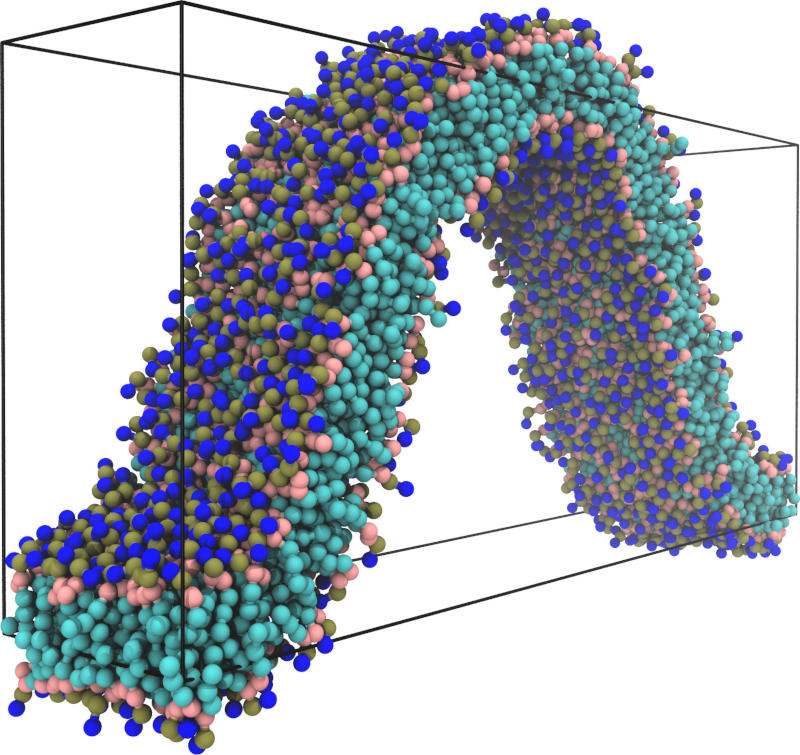
Figure 1: If a lipid membrane is placed inside a simulation box that is too small to hold it while flat, it must “buckle” into the third dimension. The force needed to hold it at some given amount of compression can be used to infer the membrane’s rigidity.

In our most recent paper [J. Chem. Phys. 154, 014704 (2021)] we delve deeper into this stiffening transition and examine how various parameters affect it. To gain insight into the process of stiffening we look at the hexatic order parameter of the lipid tails, which is a quantitative measure of how closely lipid tails form an ordered triangular lattice on the leaflet midsurface:

Figure 2: The upper image shows a cross-sectional view of a buckled membrane, in which the upper leaflet is under a higher (compressive) stress than the lower one, as it has a larger number of lipids. If for this leaflet we look at the positions of the lipid tails (two per lipid, shown as two circles connected by a line), we find that an ordered domain has formed, distinguished by a well-defined triangular lattice.

What we observe is that once number asymmetry between leaflets (a proxy for differential stress) has crossed a critical threshold, highly ordered domains resembling what is known as a lipid gel phase would form in the compressed leaflet, leading to an overall stiffening of the bilayer. In the buckle geometry we observe that these domains occur more likely in the less curved regions near the inflection points of the buckle as opposed to the highly curved maximum or minimum.

By simulating membranes at different temperatures we see a direct relation between temperature and the critical asymmetry needed for the stiffening transition to happen. We also find that the critical asymmetry increases rapidly with temperature, and this suggests that a stiffening transition can only happen within a limited temperature window above the gel-to-fluid phase transition of a lipid membrane.

Lipids with more saturated or longer tails tend to be more ordered at the same temperature and hence we would expect that they can be more easily driven into the stiffened regime compared to less ordered lipids. This is indeed what we observe in our simulations of MARTINI DLPC and POPC—two particular types of lipids, of which the latter goes through the stiffening transition at a higher value of number asymmetry than the former at the same temperature.

We also examined the effect of system size on this transition and observed that bigger systems with smaller typical curvatures are easier to be stiffened by this phenomenon. This is a good sign for the relevance of this study for real biological membranes since typical curvatures in those systems are much lower than in our simulations.

We have demonstrated that stiffening induced by differential stress in asymmetric lipid bilayers is a more general phenomenon rather than an idiosyncratic feature of the specific system examined in our earlier work. Furthermore, we have presented formation of finite higher order domains as a mechanism explaining our observations. Considering differential stress as an important parameter in the physics of lipid membranes is a novel idea and we are excited for the prospect of experimental confirmation of our observations in model systems and cell.