This blog post started as a humble thread on Twitter, which turned out to be unexpectedly popular. Several readers commented that the subject might be easier to digest in a format that’s more appropriate for long-form presentations. And so I’ve decided to port the content to this blog, too. The main theme is of course the same: I’d like to expose you to one of the many fun quirks of special relativity—velocity addition—and then try to convince you that the result is actually not quite as weird as it appears at first look. (Actually, towards the end I’ve collected a few additional thoughts, motivated by discussions that happened on Twitter. They are at a technically slightly higher level than the original Twitter thread, so you can safely skip them. Or just see how far you can ride the out!)
Intrigued? Well, then: buckle up!
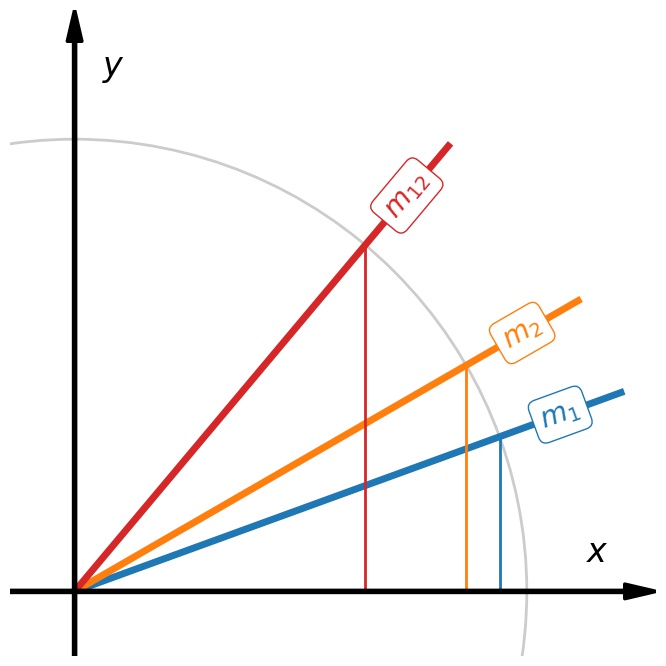
We shall begin by looking at a 2-dimensional rotation around the origin in the $(x,y)$-plane. We can quantify it by an angle $\phi$ and visualize it by a line through the origin that is rotated by that angle $\phi$.
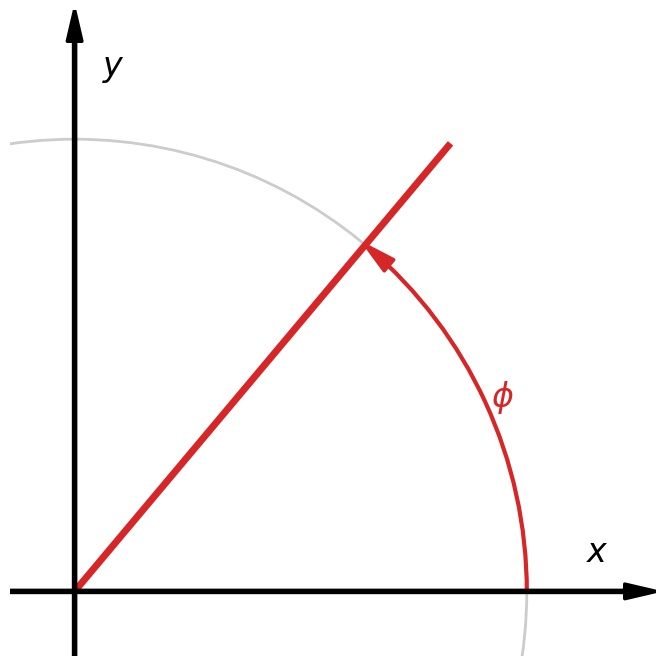
Let’s now consider two rotations, $\phi_1$ and $\phi_2$, as well as the two corresponding lines through the origin at angles $\phi_1$ and $\phi_2$. We are interested in an overall rotation $\phi_{12}$ by both angles together.
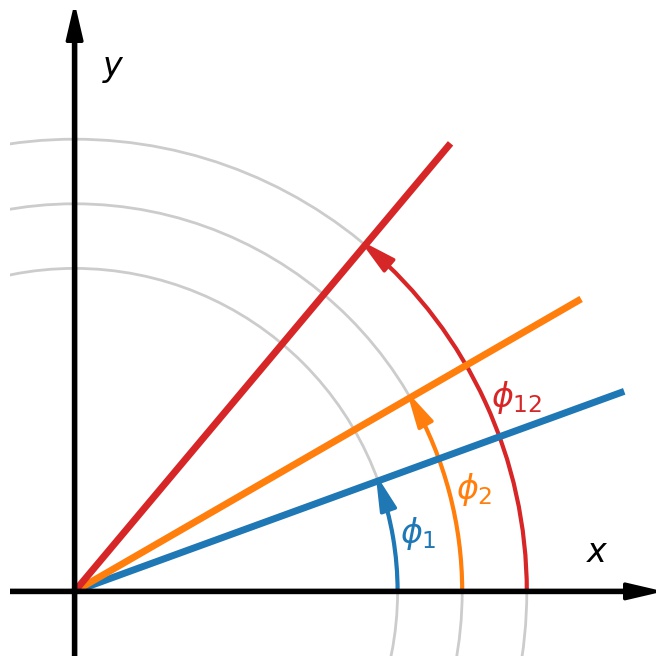
Evidently, the total angle is $\phi_{12} = \phi_1+\phi_2$. One way to see this in the image is to realize that this also implies that $\phi_2=\phi_{12}-\phi_1$, and so rotating back from the sum angle by one of the two angles gives us the other one.
OK, none of this is remotely surprising. But things get interesting if we—for whatever reason—decide to describe these rotated lines in a different way. Specifically, how about we describe these lines by their slope $m$, “rise over run”.
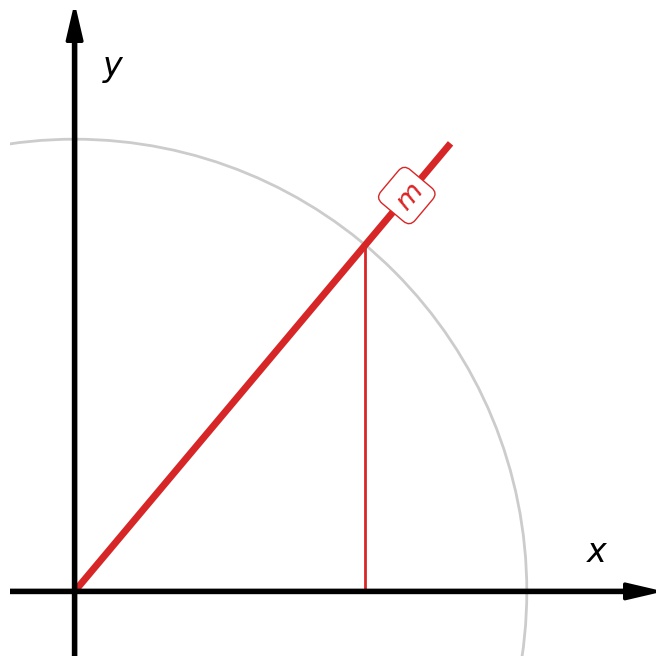
This is of course a very common way to describe tilted lines, and it has the redeeming quality that the equation for the line is dead easy: $y=m\cdot x$.
Just as before, we can now picture two lines, characterized by slopes $m_1$ and $m_2$, and ask what is the slope $m_{12}$ of the line that rotates by the sum angle? This turns out to be a much trickier question, because angles add, but slopes don’t.
Fortunately, angle and slope are related by a fairly simple relation: the slope is the tangent of the angle: $m=\tan(\phi)$. Since we know that angles add, and by exploiting some trigonometric identities for the tangent, we can find the new slope. Let’s do this!
Evidently, if $\phi_{12}=\phi_1+\phi_2$, we also have
$$\arctan(m_{12}) = \arctan(m_1) + \arctan(m_2)$$
Moreover, exploiting the trigonometric identity
$$\tan(x+y) = \frac{\tan(x) + \tan(y)}{1 \;–\; \tan(x)\cdot\tan(y)}$$
this leads to
$$m_{12} = \frac{m_1 + m_2}{1 \;–\; m_1\cdot m_2}$$
This is the formula for how rotations combine if we for whatever reason decide to describe a rotated line not by its angle but by its slope. Clearly, this looks more complicated, but we see what’s going on. Everything’s fine. We’re good!
But imagine now that we restrict ourselves to really small angles, and correspondingly small slopes. Indeed, think of $m_1$ and $m_2$ being very much smaller than 1, such that the term $m_1·m_2$ in the denominator can be safely ignored compared to the other term, 1. In this small-angle-limit the slope-addition-formula simplifies tremendously: up to a tiny correction, $m_{12}=m_1+m_2$. Slopes add! How nice! Of course, it’s just an approximation, but it surely makes life easier if we happen to be in a small angle regime.
So far so good. Now let’s go to the next step. Imagine a group of “practical geometers” who (for whatever reason) have never really dealt with large angles. (Weird, I know—but bear with me!) For practical purposes, they always work in the small angle regime. For them, $m_{12}=m_1+m_2$ always holds with excellent approximation. In fact, they might not be able to tell the difference, because it’s too small to measure. They might even start to think of this formula as being how rotations actually combine. You add slopes!
It is easy to see how they might develop some “intuition” for why this should be so. And how, as time passes, they would start to think of this formula not as an approximation but as the Truth, with a capital “T”. Habit is a powerful drug!
Until, one day, a particularly deep-thinking geometer, Al Unapietra, starts to think hard and deep about the true geometry of rotations, and he “re-discovers” the actual truth, and the more complicated formula. Everyone’s surprised. Most people are confused.
Precision measurements show that Al is right: the more complicated formula is really correct. But damnit, it is so unintuitive! Al’s discovery is simultaneously hailed as a breakthrough and as mathematical challenge too difficult for everyday people to comprehend.
Is it, though?
It’s only unintuitive if you insist on describing the rotation of lines by their slope $m$. But this is just not a very smart way of doing it if you want to add rotations! If you re-calibrate your thinking and return to the angle $\phi$, things greatly simplify!
So far, the moral of our story is this: whether things look simple or not—intuitive or not—often depends on how you describe them. If you insist on the wrong mental framework, a simple fact might look needlessly opaque.
At this point you might be asking, “Hello? Relativity? Didn’t you promise us a lesson in relativity?” Yes, I did. But I needed to prepare you for it. That’s done now, and we’re ready for the harvest!
Let’s say we have a spaceship that moves away from us at some sizable speed $v_1$. And let’s say that inside the spaceship an astronaut fires a railgun, shooting a bullet forward with velocity $v_2$ relative to the rocket. What is the bullet’s speed $v_{12}$ relative to us?
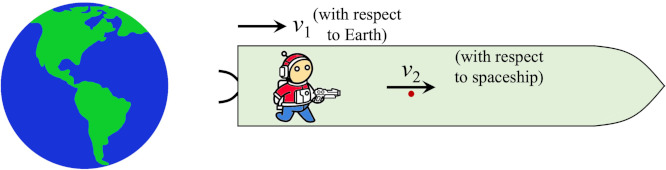
You might say, “Easy! It’s obviously $v_{12}=v_1+v_2$!” And that’s indeed what you would learn in any introductory course in classical mechanics. But the answer is wrong. If you make very careful measurements, you get a slightly different answer!
To write down what the true answer is, let me introduce one more piece of notation that is very common in relativity: we measure speeds in fractions of the speed of light, $c$, and we call that fraction $\beta$. So $\beta=v/c$, or equivalently, $v = \beta c$.
In this notation, you might expect to find
$$\beta_{12} = \beta_1 + \beta_2$$
However, the actual answer is
$$\beta_{12} = \frac{\beta_1 + \beta_2}{1 \;+\; \beta_1\cdot\beta_2}$$
Does this remind you of something? Up to a $+$ vs. $-$ difference in the denominator (I’ll get back to that later!), this is basically the same as our fancy slope-addition formula! And the beautiful thing is: this is not a coincidence! Let me explain.
It turns out that describing the motion of a “frame of reference” (e.g. a spaceship) by its speed is equivalent to describing the rotation of a line by its slope. It works, but it can get you in trouble, especially for large angles—or here: large speeds. Successive changes of reference frames, which in a “Galilean mindset” you want to think of as “adding their speeds”, really are more akin to rotations, and it’s these rotations that add, not the speeds!
“But wait,” you say, “what’s rotating?” If the spaceship moves to the right, and the railgun inside it is also fired to the right, everything happens along the same direction! Where is the rotation? Great question! And this is where relativity is really weird!
There are two qualitatively different things at play now. Let me address them one at a time.
First, the rotation is indeed not a rotation in space. It is a rotation in spacetime! Relativity insists that changes between moving coordinate systems mix up space- and time-coordinates. That, indeed, is very unexpected for our Galilean minds!
And second, I haven’t yet addressed that pesky minus sign difference between our “addition formulas”. It turns out that this is where it now matters. Our transformation is indeed not exactly a rotation. Instead, it’s a so-called “hyperbolic rotation”.
Before I tell you how to write this down in mathematical notation, let me show you what it looks like in two simple animations.
First, normal rotation. You are surely familiar with how this “works”. Here’s an animation that rotates a coordinate system by some angle $\phi$. Both axes tilt by the same amount in the same direction, and the orbits are circles.
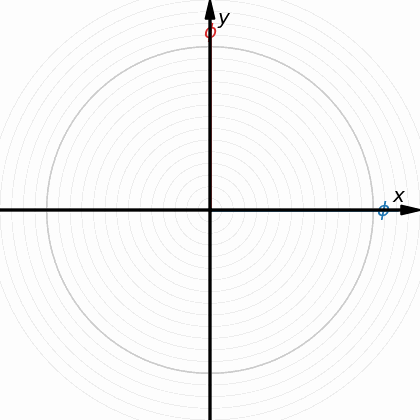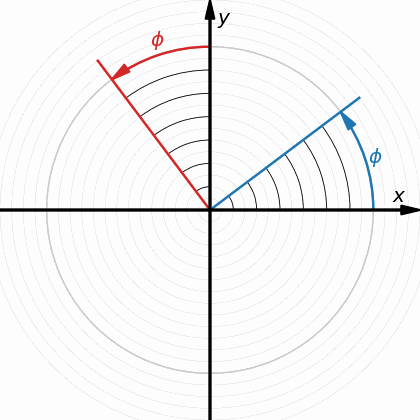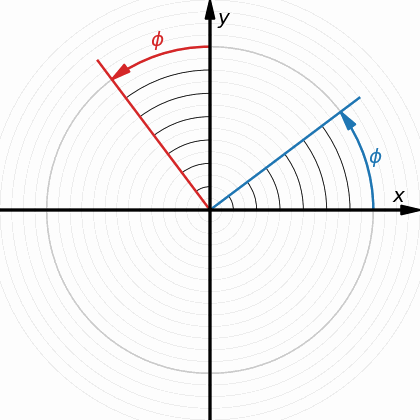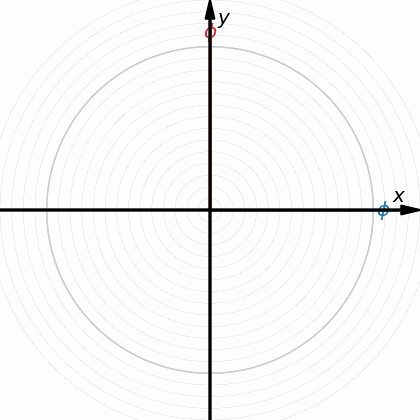
Now, hyperbolic rotation. This animation shows that, again, both axes tilt by the same amount, but in opposite directions. Furthermore, the orbits are now hyperbolas, not circles.
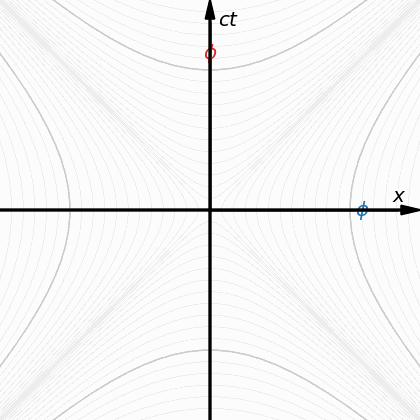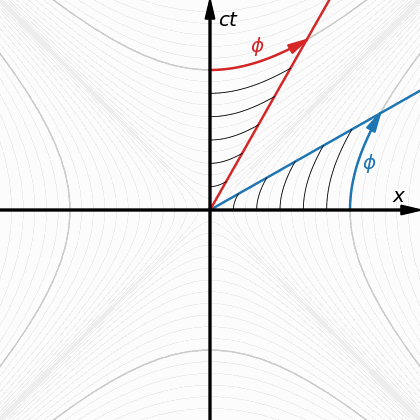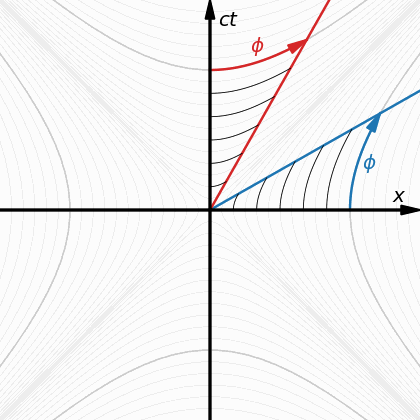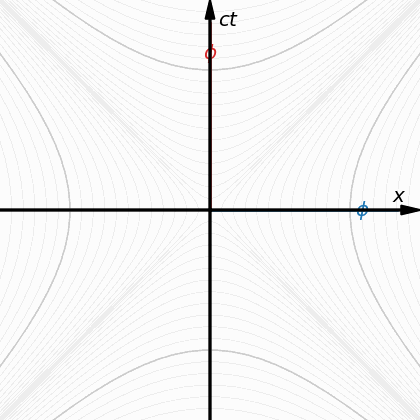
OK, this doesn’t really look like a rotation at all—so why do I call it “hyperbolic rotation”?
The reason is that it’s mathematically very similar. First, it’s a linear transformation. Second, its matrix has determinant 1. And third, that matrix even looks almost like a rotation matrix! Except all the trigonometric functions are replaced by hyperbolic ones!
For direct comparison: here’s what an (active) space rotation by an angle $\phi$ looks like—when applied to the $(x,y)$-coordinates from our above animation, and when written succinctly as a matrix equation:
$$\left(\begin{array}{c} x’ \\ y’ \end{array}\right)=\left(\begin{array}{cc} \cos\phi & -\sin\phi \\ \sin\phi &\phantom{-}\cos\phi \end{array}\right)\left(\begin{array}{c} x \\ y \end{array}\right)$$
And here’s an (active) hyperbolic rotation by an “angle” $\phi$, applied to the spacetime coordinates $(ct,x)$—i.e. speed of light $c$ times time $t$, paired up with an $x$-coordinate:
$$\left(\begin{array}{c} ct’ \\ x’ \end{array}\right)=\left(\begin{array}{cc} \cosh\phi & \sinh\phi \\ \sinh\phi &\cosh\phi \end{array}\right)\left(\begin{array}{c} ct \\ x \end{array}\right)$$
I think this is similar enough to warrant a terminology that at least “reminds” us of rotations!
It gets better: recall that in the “normal” rotation case we had a connection between angle and slope: $m=\tan(\phi)$. We also have a corresponding relation between the hyperbolic rotation angle $\phi$ and the relativistic equivalent of the slope, the scaled speed $\phi$. It is: $\beta=\tanh(\phi)$!
Again, up to a “trig goes hyperbolic” replacement, everything is identical. And since the “sum of angles” identity for tanh versus tan has a $+$ vs. $-$ difference in the denominator, that also explains the difference in our addition formulas!
Incidentally, since angles add, both for rotations as well as for relativistic changes of reference frames, the angle $\phi$ also has a special name in relativity. It’s called “rapidity”. And as far as velocity addition is concerned, we can now see: rapidities add!
You will of course not be surprised to learn that these hyperbolic rotations probably play a big role in relativity. And indeed, they do. An enormously big role. In fact, all of physics nowadays must play nicely with these rotations.
Except, they are usually not called “hyperbolic rotations” by physicists. They are called “Lorentz transformations”.
This is how far the thread went on Twitter. In the busy week after posting it, many reader made excellent comments, or asked very perceptive questions. I therefore thought I might use the reincarnation of this material as a blog post as an opportunity to add a few extra thoughts here. (After all, you made it this far—might as well get a bit more out of it than the first time around!)
- Hyperbolic rotations are Lorentz transformations, but not every Lorentz transformation is a hyperbolic rotation. The distinction is important if one thinks more about these subjects. Hyperbolic rotations are a subset of all Lorentz transformations, and they are typically called “boosts“. The idea is that they express a change of reference frame into a new coordinate system that moves with respect to the original one with some speed $v$ in some direction. So the picture is that this Lorentz transformation “boosts” you into that direction.
- This distinction matters because hyperbolic rotations lack one absolutely crucial property which normal rotations have: they do not form a “group” in the mathematical sense. The essence here is this: two subsequent rotations can always be written as yet another rotation (by some angle, around some axis), but the same is not true for hyperbolic rotations—except for the special case that we hyperbolically rotate around the same axis (or, more precisely in 4 dimensions: within the same plane).
- Transformations not forming a group is generally considered a disaster among people working with such things, because there’s like a bazillion nice properties one loses. Thankfully, things here are not quite as dire as it might seem: It turns out that two hyperbolic rotations together form another hyperbolic rotation, if you permit yourself some additional ordinary rotations to “fix” some misalignments that happen along the way. This means that hyperbolic rotations and normal rotations together form a group after all, and this turns out to be enough. It is called the Lorentz group.
- I have shown that there is a close analogy between normal rotations and hyperbolic rotations, in that for instance the associated matrices almost look alike, except that trigonometric functions are replaced by their hyperbolic counterparts. I have not told you, though, what these hyperbolic counterparts are, since I assumed most people would know. Let me briefly show you in one more set of equations how close the connections are, in case you haven’t seen this yet. Granted, this requires that you’ve seen some complex analysis before, and the odds that you have seen that but don’t know what $\tanh(x)$ is are indeed very small. But, if nothing else, take it as another pretty formula. So here we go: The hyperbolic functions $\sinh(x)$ and $\cosh(x)$ are simply defined as
$$\sinh(x) = \frac{{\rm e}^x-{\rm e}^{-x}}{2}$$
$$\cosh(x) = \frac{{\rm e}^x+{\rm e}^{-x}}{2}$$
- That basically just makes them linear combinations of the plain exponential function. (In fact, you may think of them as a symmetrization and antisymmetrization of the two functions ${\rm e}^x$ and ${\rm e}^{-x}$.) The relation to the trigonometric functions is that we can define them in exactly the same way, just with the complex number ${\rm i}$ sprinkled in there:
$$\sin(x) = \frac{{\rm e}^{{\rm i}x}-{\rm e}^{-{\rm i}x}}{2{\rm i}}$$
$$\cos(x) = \frac{{\rm e}^{{\rm i}x}+{\rm e}^{-{\rm i}x}}{2}$$
- Observe that suitably adding these two equations together shows that ${\rm e}^{{\rm i}x}=\cos(x)+{\rm i}\,\sin(x)$, which after picking $x=\pi$ leads to one of the most well known and beautiful equations in mathematics: ${\rm e}^{{\rm i}\pi}+1=0$, since it combines the 5 most important mathematical constants into a single equation.
- The fact that the imaginary number ${\rm i}$ shows up suggests that there are other ways in which we could maybe formulate the whole hyperbolic rotation and Lorentz boost spiel that will make the analogy even more perfect. Indeed, this is possible. If we formally express time as imaginary (or give ourselves an extra prefactor ${\rm i}$ in front of time coordinates), then for the most part everything just looks like rotations. Everything looks “Euclidean”, one sometimes says. However, this is a bit of a cheat, since it ends up hiding the fact that this pesky minus sign is the first inkling that the geometry of our universe has a nontrivial metric. Granted, it’s just one funny minus sign, and we can hide it with the “complex trick”; but we can only do this in empty space. Once we populate our universe with stuff—stars, planets, people—this stuff has mass and this mass causes gravity. According to Einstein’s theory of general relativity, this gravity manifests as a curvature in spacetime, and this leads to much more interesting changes of the metric. And since we can no longer save the day by the complex trick, one wonders how much one really has gained from it. One might as well treat the whole thing properly as a geometric theory with a non-Euclidean metric.

Markus Deserno is a professor in the Department of Physics at Carnegie Mellon University. His field of study is theoretical and computational biophysics, with a focus on lipid membranes.

0 Comments