A delightful pastime in mathematics is to think about really big numbers. And unlike many other mathematical mind games, this is one that has captured the imagination of a much wider community. It is fun to think about a million, a billion, or a trillion, and then picture how big they are, and how much bigger each subsequent number is than the previous one. This game is hard to continue, though, simply because we run out of names.

The next step is huge powers of ten. A thousand is $10$ times $10$ times $10$, or $10^3$. A million is $6$ such factors, $10^6$, and a billion and trillion are $9$ and $12$ factors, respectively. What if we take a hundred factors of ten? That leads to the number $10^{100}$, which is known as a googol. It is a one followed by 100 zeros. (Fun fact: this number inspired the name of the search engine Google, but the company’s founders accidentally misspelled it when checking whether the web domain was still available. The rest is history.)

To get much bigger than that, we need to put larger numbers into the exponent. Like a thousand, or a billion, or a trillion. Or, hey, why not a googol? Yes, that number exists (of course) and it has a name: it’s called a googolplex:

${\rm googolplex} \; = \; 10^{\rm googol} \; = \; 10^{10^{100}}$ .

It is indeed huge. It’s a 1 followed by a googol number of zeros! This game can of course be continued, but it’s a bit arid, since no new “mechanism” arises for making numbers bigger. So we need some novel mathematical notation.

The best way to see how this works is to look at a few examples. For the most part, this is a repeated exercise of the last rule in this set:

$$\begin{align}3\uparrow\uparrow 3 &= 3\uparrow^2 3 \\ &= 3\uparrow(3\uparrow^2 2) \\ &= 3\uparrow(3\uparrow(3\uparrow^2 1)) \\ &= 3\uparrow(3\uparrow(3\uparrow(\underbrace{3\uparrow^2 0}_{=1}))) \\ &= 3\uparrow(3\uparrow(\underbrace{3\uparrow 1}_{=3})) \\ &= 3\uparrow(3\uparrow 3) \\ &= 3\uparrow 3\uparrow 3 \ .\end{align}$$

In the last step we dropped the parenthesis, since people have agreed that the up-arrow notation should be right-associative, meaning, we parse things from right to left.

So what is $3\uparrow3\uparrow3$? Since the up-arrow denotes exponentiation, repeated up-arrows lead to a tower of exponentials, in this case:

$3\uparrow3\uparrow3 = 3^{3^3}$

Repeated exponentiation is sometimes also called tetration. It creates stacked powers of powers, and is therefore sometimes called a “power tower”.  Since $3^3 = 3\times3\times 3=27$, we see that $3\uparrow3\uparrow 3=3\uparrow27$, which means we need to multiply the number 3 with itself, 27 times. That gives rise to the number 7,625,597,484,987, or about 7.6 trillion. Wow, quite a bit!

This is now the time where we can introduce a number which breaks everything we’ve seen so far, by a lot, and which is very famous both in mathematics and in many recreational circles of mathematicians who delight in such games. Knowing it, or at least having heard of it, has become a badge of recognition for the big number aficionados. We’re talking about Graham’s number.

Graham’s number is “made” in steps, and it uses the up-arrow notation for the steps of this construction. Let us begin with a short sequence of increasingly large numbers using increasingly more up-arrows: $3\uparrow3$; $3\uparrow\uparrow3$; $3\uparrow\uparrow\uparrow3$; $3\uparrow\uparrow\uparrow\uparrow3$. These can slightly less dramatically be written with powers on the arrows, and so the last one is just $3\uparrow^43$. Each subsequent number in this series gets massively bigger than the previous one (and we will have more to say about this, hang on!). So we could just repeat this game and keep increasing the number of arrows. But the game changes at this point. First we give the last number a name, and call it $g_1$, meaning, $g_1=3\uparrow^4 3$. We then construct a new number $g_2$, which is defined as follows:

$g_2 = 3\uparrow^{g_1}3 = 3\;\underbrace{\uparrow\uparrow\cdots\cdots\cdots\uparrow\uparrow}_{g_1\;{\rm up-arrows}}\;3$ .

Wow, that escalated quickly! We now have a ginormous number of up-arrows, and given that each single added arrow makes the number massively larger, the addition of a massive number of arrows absolutely truly and breathtakingly explodes the resulting number.

But wait, there’s more!

We can now define a new number, $g_3$, as follows:

$g_3 = 3\uparrow^{g_2}3 = 3\;\underbrace{\uparrow\uparrow\cdots\cdots\cdots\uparrow\uparrow}_{g_2\;{\rm up-arrows}}\;3$ .

In other words, we have incomprehensibly increased the number of arrows, blowing things again vastly into the beyond.

And we’re still not done. We now repeat this game 61 more times! Each time creating a new $g$-number by using the $3\uparrow\uparrow\cdots\uparrow\uparrow3$ construction and taking the number of up-arrows to be as many as the previous $g$-number. This then leads to the number $g_{64}$. And that is Graham’s number!

At this point, the customary thing to do is to regale in extravagant language (and quite some hand gesticulation if done in front of a live audience) to express how mind-bogglingly big this number is. How incomprehensibly large, how utterly, blazingly, vastly gargantuan. But this is just incredibly lame rhetoric, as if human language were somehow more powerful to grasp the largeness of $g_{64}$ than the extraordinarily sleek mathematical notation we have just made use of. Or as if it would give us even the remotest sense of comprehending what is going on here. It doesn’t. And unless you are a mathematician who has specialized for their entire career on problems where such numbers arise, you will have a snowball’s chance in hell of coming close to comprehending Graham’s number. And I suspect that most of these mathematicians are also not really there with an intuitive understanding.

But what I wanted to do here is to emphasize that basically the same I-give-up feeling occurs much earlier in the sequence of making Graham’s number. We don’t have to go all the way to the terrifying end before we must give up. Yes, $g_{64}$ is really big, but the first baby-steps to get us there will already break our brain.

Let me show you how.

Recall the very first sequence of number we made? $3\uparrow3$; $3\uparrow\uparrow3$; $3\uparrow\uparrow\uparrow3$; $3\uparrow\uparrow\uparrow\uparrow3$. How big are those?

Well, the first we had already calculated: $3\uparrow3 = 3^3 = 27$. And the second we had calculated as well: $3\uparrow\uparrow3=3^{27} = 7,625,597,484,987$. What is the next one?

Using the rules from above, we find

$$\begin{align}3\uparrow\uparrow\uparrow 3 &= 3\uparrow\uparrow 3\uparrow\uparrow 3 \\ &= 3\uparrow\uparrow 7,625,597,484,987 \ . \end{align}$$

Since we already know that double-up-arrows create a power tower, we realize that this is a truly huge power tower. It looks a bit like this:

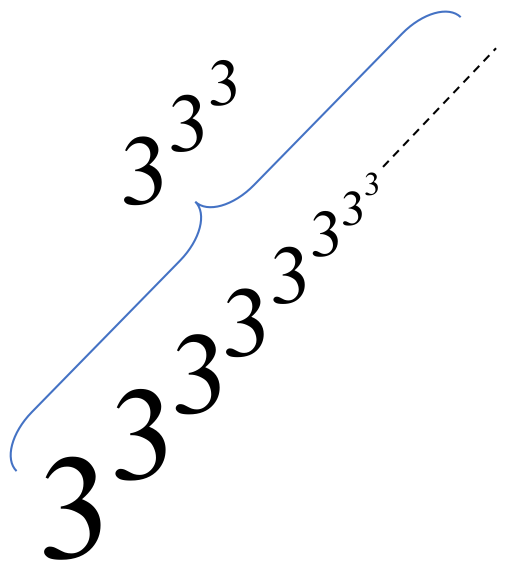
So it’s a power tower that has $3^{3^3}$ occurrences of $3$ in it, or about 7.6 trillion 3s.

And there you have it. We just broke our brain. We gave up. We lied. We threw our hands in the air and said, hell, it doesn’t matter anymore.

What? What did we do?

We said, “A power tower with about 7.6 trillion 3s.” And that’s wrong. Because it’s really 7,625,597,484,987 occurrences of 3, not “just” 7.6 trillion. But you might say, “well, these numbers are close”. But these are the numbers of 3s in a power tower! How different does our result get if we quote our result approximately? What if we, as we did, neglected more than 25 billion occurrences of 3 in that tower?

To see what that means, here’s a helpful (and shocking) procedure. Recall what a logarithm does to a power:

$\log(a^b) = b\,\log(a)$ .

It pulls the exponent out. That of course also works for power towers: it will pull the tower out. Let’s look at this in one example:

$\log\left(3^{3^{3^3}}\right) = 3^{3^3}\,\log(3)$ .

That means, we get a tower that is smaller by one occurrence of 3, and the result is then multiplied by $\log(3)$. If we take the natural logarithm, which is the most common (indeed, “natural”!) one in mathematics, then the final factor is $\log_{\rm e}(3)=\ln(3)\approx 1.099$, which is close enough to $1$ that we will ignore it in the following. (If that upsets you, then just take the logarithm with base 3, and then the factor is exactly $1$!)

So let us recap: taking the logarithm of a power tower of 3s gives a new power tower of 3s that is one 3 shorter.

This now helps us to understand why I said we hopelessly capitulated when we described $3\uparrow^33$ as “a power tower of 3s that contains 7.6 trillion 3s.” We forgot about 25 billion 3s. And that means the following: if we take the true value of $3\uparrow^33$, and then we take the logarithm of it, and then we take the logarithm again, and then again, and again, and again, … 25 billion times—only then will we arrive at a number that is “a power tower of 3s that contains 7.6 trillion 3s.” In other words, we no longer distinguish between a big number, and another big number that arises after repeatedly taking the logarithm of the first one a mind-numbingly large number of times. We treat those as “basically” the same number. And that’s why we have basically given up.

Of course, we know that applying the logarithm makes huge numbers tiny. For instance, remember googol, $10^{100}$? Its natural logarithm is approximately 230, and the logarithm of that is about 5.4. So after just taking the logarithm twice, we cut down a googol into a number that’s basically within the grasp of one hand. How about a googolplex? Taking the logarithm just three times gets us again to 5.4.

It’s really hard to conceive of numbers that are so big that a few logarithms wouldn’t cut them to size quite handily. For instance, take the smallest conceivable volume in the universe, the smallest one where we still feel that our current laws of physics apply: the Planck volume. It’s a cube with a side length of about $1.6\times 10^{-35}\,{\rm m}$. And now take the observable universe itself: a sphere with a radius of maybe 46.5 billion light years. How many Planck volumes fit in there? Answer: about $9\times 10^{184}$. That’s bigger than a googol, but a lot smaller than a googolplex, and so just two applications of a log would cut it to size. In fact, it would give us a value of about 6. What if we now imagine that each such volume can hold one bit of information? How many possible states could the universe contain? Answer: $2^{9\times 10^{184}}$. That’s bigger than a googolplex! But three successive logs cut it to a convenient size, again to about 6. We’re not getting anywhere here!

And now imagine a number so big that you can’t really bother to distinguish whether or not you took its logarithm 25 billion times.

See: you can’t imagine that. That’s my point.

And, I’d like to remind you that we haven’t even completed the last baby-step towards constructing Graham’s number. We haven’t even arrived at $g_1$, which is four up-arrows flanked by 3s! We can’t even handle the case of three up-arrows without giving up! And since the case of two up-arrows was very much within our grasp, that tells you how frightfully much bigger $3\uparrow^43$ must be compared to the already incomprehensible $3\uparrow^3 3$. And all of that happened before the explosion of $g_1$ up-arrows. It’s just hopeless.

The trouble is that most of us have no intuitive understanding of processes that would grow more rapidly than exponentiation. Of course, these exist in mathematics, where situations can be contrived where they show up. A famous subfield that is infested with such processes, and correspondingly huge numbers, is “Ramsey theory”—a branch of combinatorics that looks for certain patterns in substructures of bigger structures, and often asks questions such as: how big does a substructure have to be so that a certain property holds? Let us make one example.

Take a hypercube in $d$ dimensions and connect every corner point with every other corner point by a line. Now color each of these lines either red or blue. That’s our “big structure”. We’re now defining our substructure: pick 4 corner points out of the big structure, but pick them such that they are in a plane. They are connected by 6 lines, which are typically some mixture of red and blue lines. But we like order, and so we want to find a set of 4 such points so that the six lines all have the same color. Can we?

It’s not obvious, because we have no control over the original coloring. Maybe the person who colored the hypercube and its edges was particularly mean in the coloring strategy, such that simply no planar quartet exists that is of one color. But then, is that possible? Is it possible to create a coloring that has no unicolor quartets? Presumably that depends on the dimension $d$, and that’s exactly the point.

We know now, and that’s a famous theorem due to Ron Graham and Bruce Lee Rothschild, that for sufficiently small dimension, the person who colors he graph can always find a way to thwart our ability to ever find a unicolor quartet. But if the dimension is high enough, that mean spoilsport will not succeed in frustrating us, because no matter how they color the edges of the hypercube, we will always be able to find a unicolor quartet!

So how big is that mysterious dimension $d^\ast$ where we will always find that quartet? Well, that’s the hard question! And the answer is: nobody knows! But we do know that it exists, and we know lower and upper bounds—which are the content of the Graham-Rothschild theorem. These two mathematicians first proved that $d^\ast$ has to be at least 6. Later, Geoffrey Exoo showed it must be at least 11, and Jerome Barkley showed that it must be at least 13.

And what’s the upper bound? At what dimension can we be sure that we will find a unicolor quartet, no matter how fiendishly the hypercube’s edges were colored? Well, one of the well know upper bounds is Graham’s number! At that number of dimensions you can be sure that the search will be successful! But that’s such a huge number! Well, that is the trouble with Ramsey theory! It has a habit of creating formidable combinatorial problems which can only be attacked with comparatively blunt instruments, which then lead to bounds that may be ludicrously large, and maybe also ludicrously far off. Graham and Rothschild later improved the bound, and made it much smaller. Recently John Mackey, a colleague of mine in the Department of Mathematical Sciences at Carnegie Mellon University, together with two other coworkers, reduced the upper bound to $2\uparrow\uparrow\uparrow 6$, which is a massive improvement, even though still enormously large! As best as we know, the upper bound might be much smaller. Like, a lot smaller. Say, 20. (But it likely isn’t.)

That’s it for today. Now you know a bit more about Graham’s number. But I hope you also took away the idea that already the first modest baby-steps towards it basically break everyone’s brain. And isn’t that impressive all by itself?

Markus Deserno is a professor in the Department of Physics at Carnegie Mellon University. His field of study is theoretical and computational biophysics, with a focus on lipid membranes.